「 星形正多面体 : Kepler–Poinsot polyhedron 」

正多面体は、最も美しい対称性をもつ立体です。
すべての辺が合同の正多面体でできていて、各辺に集まっている面の数が同じ立体です。厳密な正多面体は5つしか存在しません。これはギリシャのプラトンの時代には証明されている事実です。
しかし、後の時代の幾何学研究において、正多面体の概念を拡張する試みが行われました。
正多角形、正多面体どちらも、頂点の数が決まれば図形の形が決まってしまいます。
例えば、正五角形といえば下記の図形一つしか存在しません。
ではここで、正多角形の「決まりごと」をすこし緩めてみましょう。
正多角形は、全ての辺の長さが等しく、全ての内角の大きさが等しい多角形のことです。そのことを踏まえつつ、下記の図形を見てみましょう。
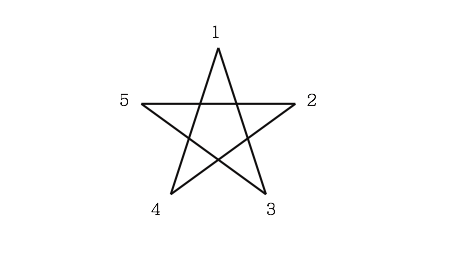
これは五芒星と呼ばれる図形です。この図形も、5つの頂点があり、全ての辺の長さが等しく、全ての内角の大きさが等しい図形です。「辺が交わっている」という一つの条件に目を瞑れば、五芒星も正五角形と考えることができます。
では広い意味での正五角形である五芒星を使って正多面体を作ってみましょう。
12の各頂点に、五芒星が5枚が集まる図形を作ると、小星形正十二面体という図形ができます。(イラスト内の星形の立体がそうです)
「面が交わっている」という条件を無視すれば、この小星形正十二面体も正多面体とみなすことができるのです。
小星形正十二面体は、16世紀に天文学者ヨハネス・ケプラーが発見した図形です。
19世紀には、この緩やかな定義の正多面体、星形正多面体は全部で4つしか存在しないことが証明されています。


