ペンローズ・タイル : Penrose tiling

どのような図形なら、平面を隙間なく埋め尽くすことができるのか?
有限個数の図形で平面を埋め尽くす操作を平面充填といい、その方法を探すことは古代から数学者、建築家、芸術家の関心事でした。
ペンローズ・タイルは、数学者のロジャー・ペンローズが1970年代に発見した平面充填の方法です。「ダート(矢)」「カイト(凧)」と呼ばれる2種類の図形で平面を埋め尽くすことができます。
このペンローズ・タイルには周期性がありません。並べていくと、どうしてもその都度並べ方を変えなければならなくなります。
ペンローズ・タイルは、黄金比とも関わりの深い平面充填です。部品であるダートとカイトは、辺の比率、そして面積の比率も黄金比になっています。そしてこのタイルを無限に近く広げていくと、ダートとカイトの枚数の比率が限りなく黄金比に近づいてゆくのです。
そして、ペンローズ・タイルは見ての通り五角形を基調としているゆるやかな5回対称(360度回転すると5回一致する)の図形です。正五角形で平面を並べるとどうしても隙間が空いてしまうように、5回対称での平面充填は。簡単ではありません。
不思議なことに、数学界でペンローズ・タイルが発見された約10年後、自然界にもペンローズ・タイルが発見されたのです。結晶学において結晶と非晶質の間に位置する「準結晶」という全く新しい「物質の状態」が発見されました。そのアルミニウムーマンガン合金の準結晶は、驚くべきことに五回対称と非周期性を兼ね備えていたのです。まさに自然界に存在するペンローズ・タイルでした。
虚数 : imaginary number
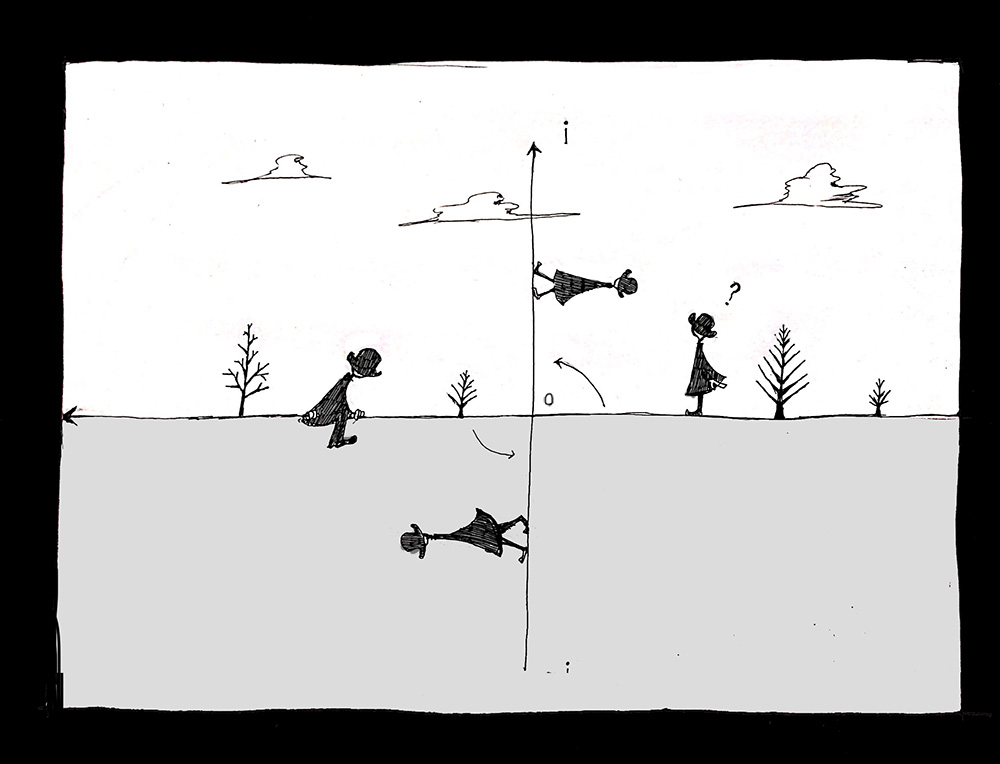
虚数は、二乗すると負の値になる数です。
その代表は虚数単位「i」で、i×i=−1となります。
身の回りにあるあらゆる数は、二乗すると正の数になります。そのため、何世紀ものあいだ数学者たちは、二乗すると負の値になる数など存在しないと考えてきました。虚数の歴史が始まったのは、16世紀のヨーロッパです。その頃になって初めて、計算式に虚数を登場させたり、虚数を数学的に定義したりして、少しづつ虚数の存在が知られるようになりました。
多くの数学者は、それでも「虚数」という存在を信じることを躊躇しました。虚数(imaginary number =想像上の、架空の数)という名前をつけたライプニッツもその一人で、この用語にも一種の侮蔑が込められていたと言われています。
しかし、その後の、数学、物理学の発展は、虚数なしにはありえませんでした。相対性理論、電子工学や流体力学、量子力学等の計算をするのに虚数は必要不可欠だったのです。
現実世界の出来事を確率で表してるシュレディンガーの波動方程式も、虚数を使って表現されています。この世界の根底には、確実に虚数が存在しています。


