「接吻数 : kissing number」

接吻数とは一つの次元に一つしか存在しない数です。
二次元の接吻数を求める場合、まず一つの円を平面上に置きます。その周りを同じ大きさの円で囲んでいきます。
周りの円は、常に中心の円に接するように、つまり「接吻」するようにし、さらに円同士が重なり合わないように並べます。その時、中心の円を囲むことができる最大の円の数は「6」です。この「6」が二次元における接吻数です。
三次元の場合、円は球となります。一つの球の周りを、常に接するように球で囲んでいきます。まず二次元の時と同じように、中心の球を6個の球で囲んで六角形を作ります。その上に3個、下にも3個、合計「12」個の球で囲むことができます。この囲み方が最も効率の良い並び方であり、「12」が三次元の接吻数です。
他には4次元、8次元、24次元での接吻数が確定されています。
4次元は24、8次元は240、24次元では19656です。
「雪の結晶 : snow crystal」

雪の結晶は、六角形の花のかたちをしています。
それだけではなく、針状のもの、弾丸型のもの、鼓型のもの、さまざまな形の結晶があります。しかし、それらさまざまなかたちの結晶も、すべて六角形を基にした形です。
雪の結晶における「六角形」とは、何なのだろうか。その疑問に初めて真剣に取り組んだのは、天文学者として有名なヨハネス・ケプラーでした。まずケプラーは、雪の結晶を形成する粒子がどのように並んでいるかを考えてみました。それらの粒子は、同じ個数で最も小さい体積になるように、最も効率的な並び方をしていると予想したのです。その並び方は、上記の3次元の「接吻数」12となる並び方と同じものでした。1つの球を中心に作った六角形を、蜂の巣のように延長させる並べ方です。ここに現れる「六角形」と、雪の結晶の「六角形」に、なにか関係があるのではないかとケプラーは考えました。ケプラーは、雲の中で雪の結晶が形作られる時に、球形の雨粒が雲の中でぎゅうぎゅう詰めになり、(まるでぎゅうぎゅう詰めの柘榴の実が変形してしまうように)、最も効率的な「六角形」のかたちに変形してしまうのだ、と考えたのです。
しかし、このケプラーのユニークな考えは間違っていたことがわかりました。X線検査により、雪の結晶の分子構造が見えるようになったのです。
雪とは、上空で気体でいられなくなった水が固体化したものです。水はご存知の通りのH2O、酸素原子一つに水素原子二つで構成されています。水が結晶となるとき、酸素は元々持っている二つの水素に加え、他の分子から二つの水素を共有して、計4つの水素を持つことになります。それら4つの水素が、できるだけ離れて酸素の周りに配置されます。すると、どうなるでしょうか。4つの水素を4つの頂点と考えたとき、出来上がるのは4つの正三角形を面とする図形、正四面体です。これが雪の結晶の基本図形になります。
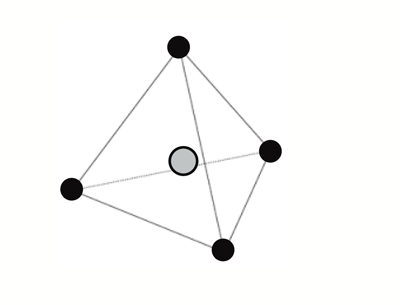
では、この正四面体を隙間なく並べていくと、どうなるでしょう。なんと「六角形」が現れるのです!
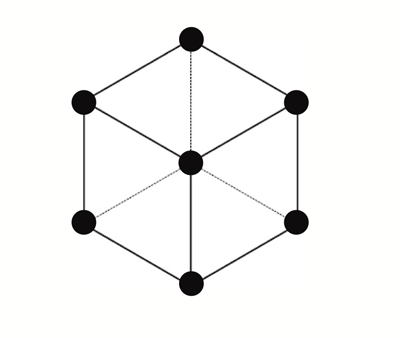
正三角形を六つ、一つの頂点を共有するように並べると六角形が現れるのを想像できるでしょう。それはつまり、ケプラーの考えた最も効率の良い並べ方と全く同じものが出来上がるのです。ケプラーの考え方は正解ではありませんでしたが、「六角形」に関する直感は間違っていなかったのです。


