「オイラー線」
レオンハルト・オイラー(1707-1783)は、これまでで最も多く、広範囲に成果を残した数学者と言われてます。その興味は数論、解析学、幾何学、そして物理学や天文学にまで及んでいました。彼の全集を作る計画は未だに完了しておらず、その全体は70巻にも登るだろうといわれています。
オイラーが残した数多くの成果の中に、シンプルで美しい一本の線があります。
その線を観察するためには、まず、任意の三角形を用意します。
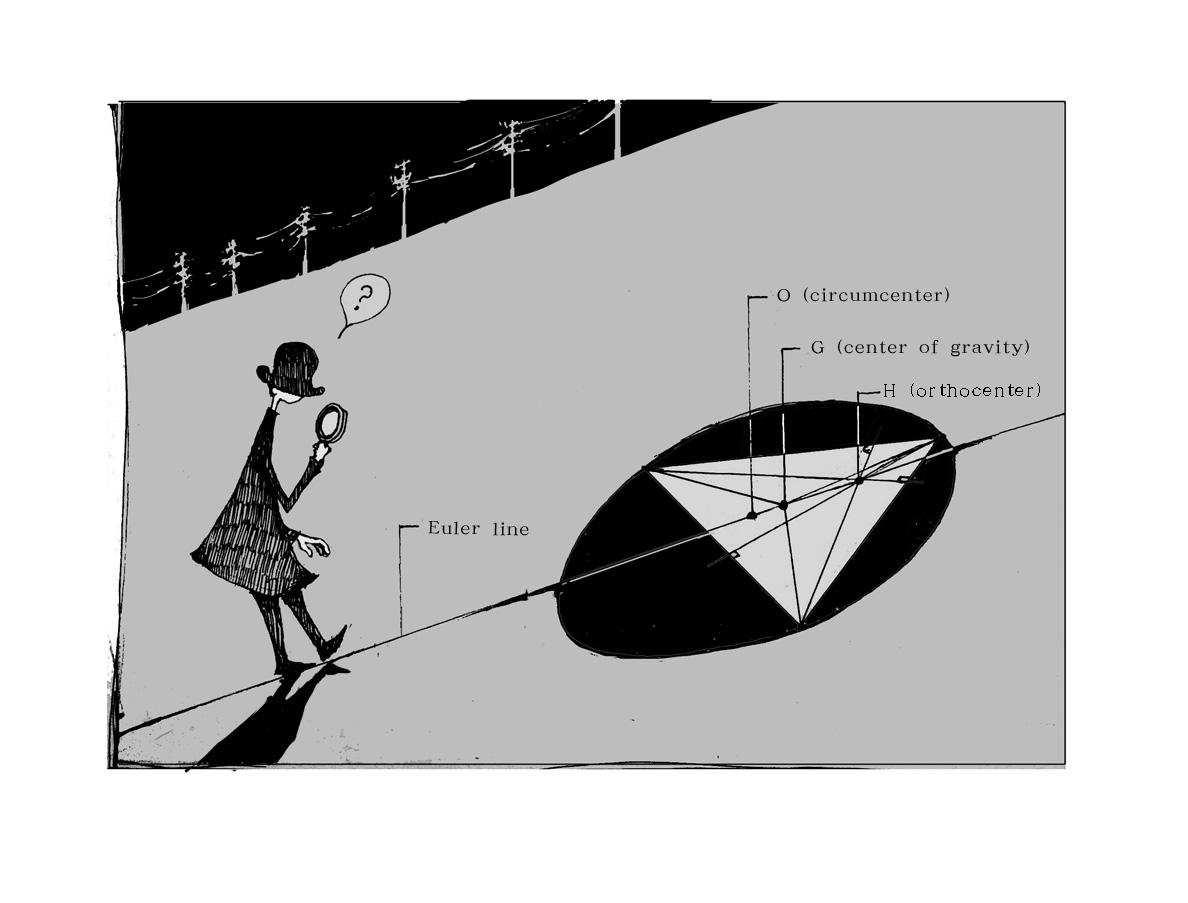
その三角形に外接する円を描き、その円の中心を「点O」とします。(外心)
次に、それぞれ辺の中心点と、その向かいの頂点にそれぞれ線を引き、交わる点を「点G」とします。(重心)
さいごに、それぞれの頂点から向かい合う辺にそれぞれ垂線を引き、交わる点を「点H」とします。(垂心)
この三点O,H,Gの座標を求めると、この三点をつなぐ一本の直線があらわれます。これが「オイラー線」です。
驚くべきことに、どのような三角形を用意したとしても、この三点は同一線上存在し「オイラー線」があらわれるのです。
ユーグリットの「原論」に収められていても不思議でないほどのシンプルなこの定理は、1765年にオイラーによって発見されるまで誰も知らなかったのです。
「モーリーの定理」

もうひとつ、1899年まで秘められていた美しい定理をご紹介します。
フランク・モーリー(1860−1937)が発見したこの定理も、まず任意の三角形から始まります。
任意の三角形を一つ用意し、その三つの頂点を三等分する線をそれぞれ引きます。
そして各辺に近い線同士の交点3つを点P、Q、R とします。するとこの3点は正三角形を形作ります。
どのような三角形を用意したとしても、その中には必ずこの正三角形、「モーリーの三角形」が潜んでいるのです。
すべての三角形に潜んでいたこの「モーリーの三角形」は、1899年に発見されるまで誰にも知られていませんでした。
今この瞬間にも、驚くほどシンプルで美しい真実が、だれも知られていない場所で息を潜めているのかもしれません。


