今月は、量子力学のお話です。
量子力学は、知れば知るほど理不尽で、つかみどころがありません。
その、もやもやとした納得のいかなさを、少しだけでも共有できたら、という試みです。
しばらくお付き合いくださいませ。
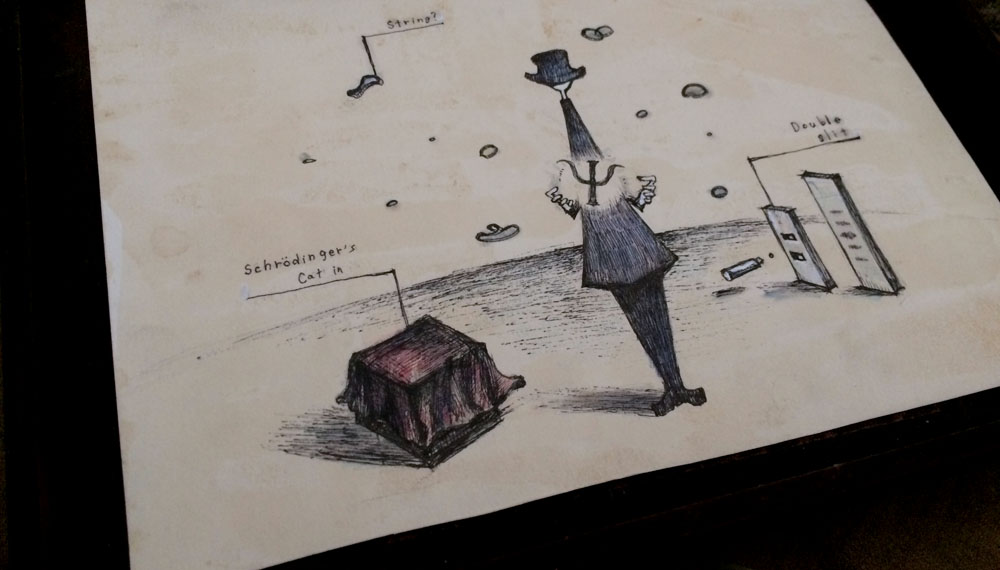
義務教育で習う「力学」は、すべて「古典力学」です。
ニュートンの発見した単純明快な法則、慣性の法則、作用反作用の法則、万有引力などによって、様々なものの動きを説明できます。どの方向に、どのくらいの重さのものを、どれくらいの強さで投げれば、何秒後にどこに到着するか、ということを計算によって正確に求めることができるのです。ロケットを月に送ることだって可能です! しかし、極小の世界、原子の内部で起きるような出来事では、古典力学とはまるで違った振る舞いをすることが分かってきました。ニュートンの考え方では太刀打ちできません。まったく新しい力学が必要です。
1900年、マックス・プランクは、ニュートン力学とは違う極小の世界での動きを説明するために、「量子論」を考え出します。「量子」とは、物理量の最小単位です。極小の世界では、各数値が不連続に、とびとびの値を示します。全ての質量、距離、エネルギーも、「量子」の整数倍で成り立っていることになります。これは、ブラウン管に映し出された滑らかな動きの映像を拡大して見たとき、点の集まりであることがわかった、ということと似ています。
私たちは、デジタルデータ化されていない現実世界を「アナログ」だと考えています。
しかし、現実の世界を拡大して拡大して拡大していけば、量子の整数倍で構成された「デジタル」であったのです。
この量子の世界での出来事を説明するため、いくつかの計算方法が考え出されました。ひとつは1926年にエルヴィン・シュレディンガーの発表した「シュレディンガー方程式」です。ふつう、方程式には、求めるべきx、yなどの未知数があります。シュレディンガー方程式ににおいて求めるべきは「ψ : プサイ、プシー」で表される「波動方程式」です。一つの素粒子の現在の状態、位置、重さ、など必要な情報をシュレディンガー方程式に入力すれば、「波動方程式」が出てくる仕組みになっています。
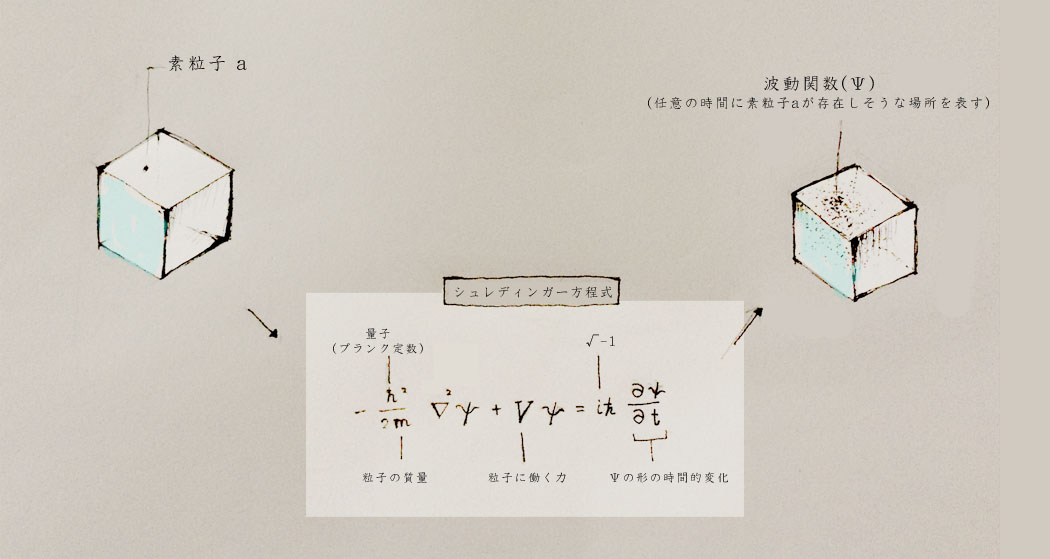
「波動関数:Ψ」これが実に奇妙で、実態がつかめない代物なのです。
仮に、素粒子aで考えてみましょう。素粒子aの現在の位置、重さ、動いている速さ等をシュレディンガー方程式に当てはめてみます。すると、任意の時間の、素粒子aの状態がわかる波動関数が出てくるのです。この波動関数でわかるのは、素粒子aが、任意の時間の、任意の位置に、どれくらいの「確率」で存在するか、ということのみです。
これはどういうことでしょう。実在する粒子であるはずの素粒子aが、時間の流れに沿って広がる可能性の”もや”のようなものになってしまうのです。これは古典力学とは全く違う振る舞いです。
しかし、ここでさらに訳のわからないことが起きます。
実態のない、可能性の”もや”のような素粒子aを、私たちが実際に「観察」するなら、その可能性の一つが瞬時に採用され、実在する粒子として、素粒子aが現れます。
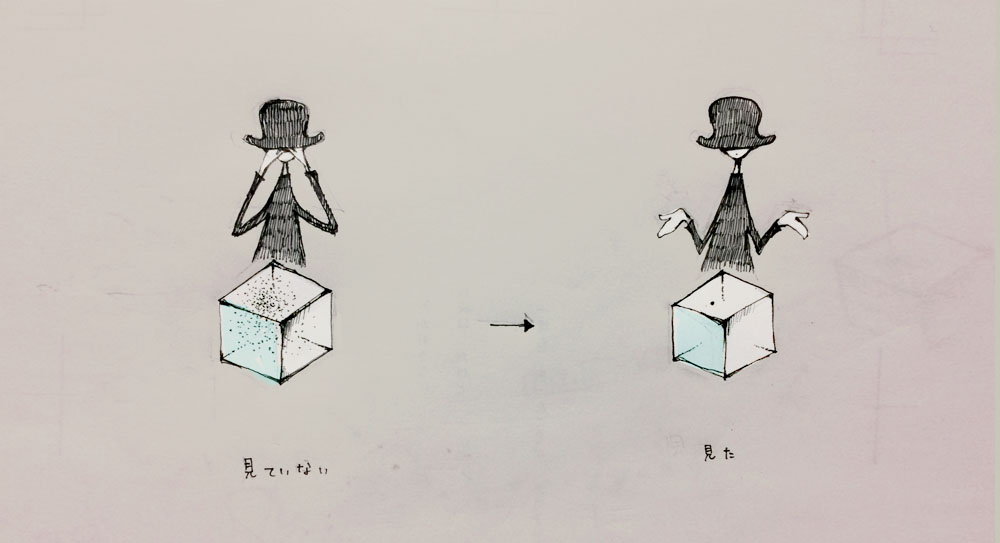
これは信じがたいことです。
「観察」とは、私たちが「見る」とは、どういうことなのでしょう?
ただ「見る」ことが、対象に影響を与えるのはなぜでしょうか?
数ある可能性の中から一つを選び出しているのは、一体誰なのでしょうか?
数学的な存在でしかない波動関数から、魔法のように実在へと変化するとき、実際に何が起こっているのか未だにわかっていないのです。量子力学の、ほんの入り口に立っただけなのに、理解しがたいことだらけです。それでも、波動関数は実用的であり、量子力学を利用した量子コンピューターも開発が進んでいます。量子力学が、抽象的すぎ、受け入れがたく思うとしても、それらを根本的に覆す理論が発見でもされない限り、現時点では受け入れざるを得ません。身の回りにあるすべてのものも、自分自身も、この不思議な性質を持つ素粒子で構成されています。それらの現象を観察し、計算を進めていくことで、想像もしなかったような、避けようのない奇妙な結論にたどり着いてしまうのです。
これはフィクションではなく、今私たちが生活しているこの宇宙でのお話です。
参考文献
朝永振一郎 「物理学への道程」(みすず書房)
ジム・アル・カリーリ「見て楽しむ量子力学の世界」(日経BP社)
日置善郎 「量子力学 -その基本的な構成-」(吉岡書店)
( 自分は物理の専門でもなく、こういったジャンルに興味があって本を読んでいるだけの者です。思い違いや情報の偏りがあったり、最新の情報と食い違うことも十分考えられます。明らかな誤りがあった場合は指摘していただけると大変ありがたいですし、説明の未熟さから余計わけがわからなくなったという方は、図書館の「物理」の棚の前に立ち、良書との出会いの機会としてください。)



