
当番ノート 第12期
近ごろ絵が描けない日が続いているのです。 とくにそれが仕事だとかそういう身分ではないので、 絵が描けなくても、とたんにご飯が食べれないとかじゃないのですけれど、 それでも絵が描くのが好きなので、そういうときは辛いです。 ぼくの好きな映画で魔女の宅急便というものがあります。 そこに出てくる絵描きの女の子が、絵が描けないとき、 「描くのをやめる。散歩したり、景色を見たり、昼寝したり、、何もしない」 と…

当番ノート 第12期
自分の中に入っていくのが好きなんだとおもいます。 なので扉がひつようです。 中の世界も、外の世界も、どちらも同じくらい大事。

当番ノート 第12期
夢から覚めて 朝がはじまる 眠りについて また夢を見る 曖昧ではあるけれど 確実にそこにあった時系列を纏めた写真集「紐解く」を2012年に作成しました。 その中から断片的にいくつかの写真を。 点と点 そのあいだを埋めていく 確かでいて不確かな 曖昧な時系列 ここにあるもの その先に見える光 それぞれの一日がある

当番ノート 第12期
コンコン ぴとぴとと、アパートメントの外縁をなぞり垂れる雨音を遮るように 少し強めのノック音が入り込みました。 「こんにちは」 見るからに優しそうな男の人が扉から顔を覗かせると、 みみこちゃんが「げっ」とでも言いたげな顔をしたので ねこたくんはほんの少しだけ不思議に思いましたが、 「かずとさんですね。さあこちらへどうぞ。」 といつも通りの顔をして、客人を室内へ招き入れました。 「やあ、元気だった?…

長期滞在者
引っ越しをした、という話の続き。 大量の本の移動の際に、昔読んでいた本に再会しました。これまでも転居を繰り返して来たけれど、その度に古いアルバムに見入ってしまったり、昔夢中になってた何かに再会して、荷物の整理作業がその度中断します。皆さんもそういう経験ありますよね。 20年以上前に良く読んでいた二冊の本が出てきました。宮脇俊三の「最長片道切符の旅」野田知祐の「日本の川を旅する」。懐かしくなって、最…

当番ノート 第12期
アドバルーンというバンドで、インドネシアまでライブをしに行くっていうので、 その日は朝5時に起きる羽目になった。 まったく良い迷惑だ。 前日の仕事が遅かったせいで、二時間しか寝ていない。 酷い低血圧なので、寝起きがとにかく悪い。 三十分で仕度するために、無理矢理身体を起こし、冷蔵庫のミネラルウォーターをガブ飲みする。 俺は東京人でも無いのにミネラルウォーターを飲む様な輩が大嫌いなのだが、 彼女と同…

当番ノート 第12期
皆さんの故郷はどこですか? この質問でどういう答えが返ってくるのか、とても興味があります。 僕にとっての故郷はずっと住んでいる名古屋ですが、第2の故郷は大阪です。 母親が大阪出身ということで、高校に入るまでは長期連休のたびに大阪へ行っていました。 春休み、GW、夏休み、冬休みと合計すると1年のうちの2ヶ月以上も滞在していたことになります。 大阪という土地が無性に好きでした。 土地柄、おっちゃんらの…

当番ノート 第12期
ある日、カレーを作ろうと思ったのです。 大阪に住んでいたとき、好きなカレー屋さんがあって、 おいしいなあ、といつも食べてたのです。 そこのカレーは20種類のスパイスを使ってました。 その日もそのお店で、 おいしいなあ、と思いながら食べてたのですが、 ふとお店のキッチンに目をやると、 たくさんのスパイスが瓶に詰まっていて、 いろんなかたちの種だったり、色とりどりの粉になっていたり、 はて、あれが、こ…
当番ノート 第12期
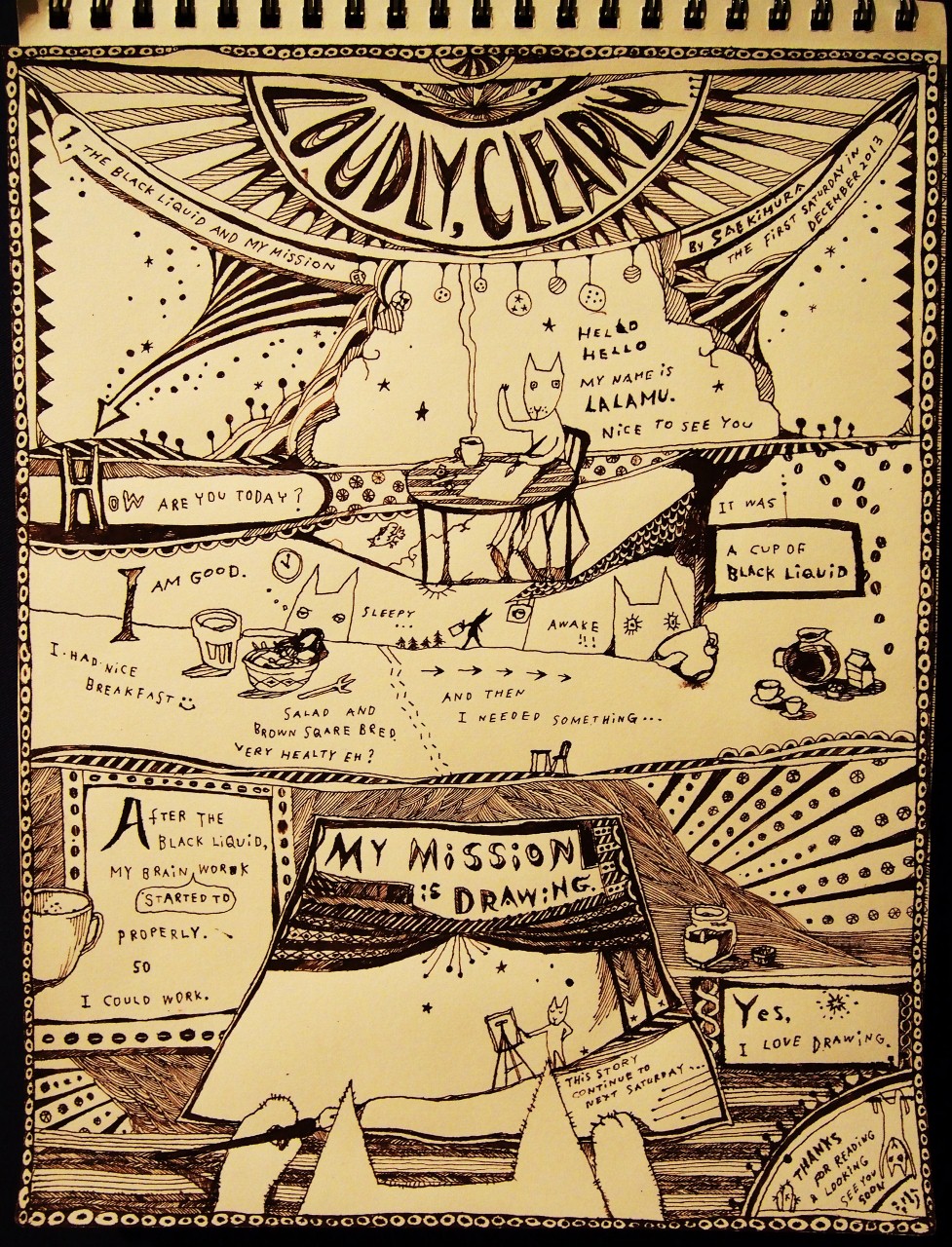
みなさんこんにちは はじめまして loudly,clearly ’おおきな声で、はっきりと’ 最近の目標です。 不自由な分、言葉がまっすぐにでてくるので、 かたことの英語で書かせてもらいました。 ・・・・・・・・・・・ わたしの使命は絵を描くことです。 すごく好きだからね。 よくがんばれます。 みなさんの毎週土曜のお楽しみになりますように ∞ sae

当番ノート 第12期
愛猫むぎお 愛称むーさん 彼は空き地に舞い降りた天使なのかもしれない むぎおは日々のんびりと暮らしている。 私の起床と共に目を覚まし ごはん頂戴と 朝のご挨拶。 ニャー。 お腹いっぱいになると家中を軽く偵察し、毛づくろいをし、 目の前を行き来している私にちょっかいを出したりしている。 一通りのことを終えると 仰向けにの格好になり またゴロゴロ。 寝転んでばかりいるむぎおだが ご主人様のお見送りは日…

風景のある図鑑
「 ビュフォンの針の問題:Buffon’s needle problem 」 平面の上に10cmの間隔で何本かの平行線を引きます。 その上から、間隔の半分の長さ、5cmの針を落とします。 落とした針が線に触れるか、触れないのか。 その針が線に触れる確率は1/πになります。 πはご存知の通りの円周率、直径を1とした時の円周の長さです。 針を投げた時に線に触れるかどうかという、円と何の関係…

