「ケーニヒスベルクの橋の問題」

かつて、プロイセン王国の東にケーニヒスベルクという大きな街がありました。その街の中央にはプレーゲル川が複雑に流れており、たくさんの橋がかかっていました。ある日、ケーニヒスベルクの住人が考えました。
「このたくさんある橋の全てをそれぞれ一度だけ渡り、元の場所に戻ってくることができるだろうか?」
多くの人がこの問題を解決しようと様々な方法を試しましたが、全ての橋を渡りつつ元の場所に戻ってくることができた人は一人もいませんでした。そしてついに、このことが数学者のレオンハルト・オイラーの耳にも入ります。オイラーは、この問題を数学的に解決できないかと考えました。そして、この問題が「一筆書き」の問題であることに気づきました。ケーニスベルクの地図を単純化すると、下の図のようになるのです。
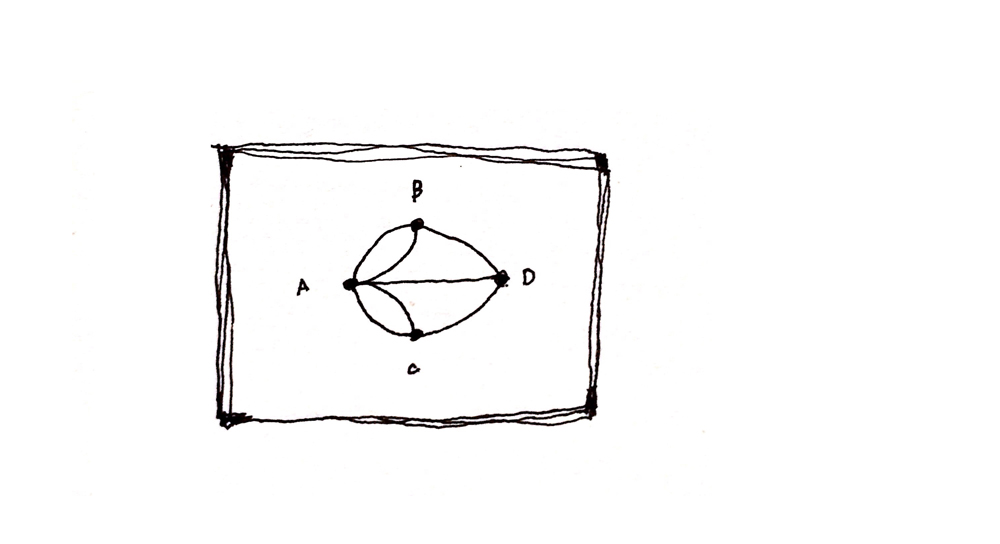
もしこの図の一筆書きでなぞることができるなら、ケーニスベルクの橋を全て渡って元の位置に戻ることができる、ということになります。どうすれば、この図形が一筆書きできるかどうか判るのでしょうか? それは、それぞれの点から出ている線の数を数えれば判断できるのです。
一筆書きできる図形とは、
①各点から出ている線の数が、すべて偶数である
②出ている線の数が奇数である点が2点だけである
どちらかとの条件を満たす図形です。
①の場合はどの点から始めても、②の場合は線が奇数になっている点から始めるなら必ず一筆書きができます。それ以外の図形は決して一筆書きができません。
それらを踏まえて、上の図を見てみましょう。点Aから出ている線が5本、点B,C,Dから出ている線が3本、全ての点から出ている線の本数が奇数です。つまり、この図は一筆書きできないことが判ります。そしてケーニスベルクの橋を全て渡って元の位置に戻ることは絶対にできないことも数学的に証明できたのです。
オイラーは、現実的な問題を極限まで単純化、抽象化することで問題を解決しました。これこそが数学の美しさであり、強みでもあります。そしてこのオイラーの考え方はのちに、「トポロジー」といわれる幾何学の一分野に発展していくのです。


